Оглавление

1. Сила притяжения внутри диска

2. Построение пробных диаграмм

3. Подбор функции плотности

4. Функция массы диска М(r)

Выводы

1. Сила притяжения внутри диска

В результате астрономических наблюдений выяснилось, что звёзды на краю галактик движутся быстрее, чем этого требуют законы Кеплера. Скорости звёзд обобщённо описываются так называемой кривой вращения, то есть, зависимостью скорости объекта от его удалённости от центра галактики. Согласно кривым вращения, звёзды с такими скоростями попросту должны покинуть галактику, но этого не происходит.

Некоторые галактики представляют собой диск переменной толщины, напоминающий скорее спортивный снаряд – диск или две шляпы приложенные друг к другу. В общем случае такой диск галактики можно рассматривать как объект, имеющий разную плотность, в зависимости от удалённости от центра.

Далее мы рассмотрим гипотетическую структуру, некое условное подобие галактики: тонкий, с нулевой толщиной пылеобразный диск радиуса R0, внутри которого находится точечное тело массой m. Никакой привязки к реальной галактике мы не делаем. Под пылеобразностью диска подразумевается возможность для тел, находящихся внутри него, беспрепятственно двигаться независимо от других его компонент.

Основной целью наших вычислений, исследований является определение возможности по заранее заданной произвольной кривой вращения сформировать такую функцию плотности, которая, собственно, и формирует эту кривую вращения. Если такая процедура возможна, то мнение о том, что движение звёзд на окраине галактик не-кеплеровское, следует, по меньшей мере, признать неточным. Также это будет означать, что такие скорости и вообще любые скорости напрямую связаны с функцией плотности дисковой галактики.

2. Построение пробных диаграмм

Рис.2.3. Диск с гиперболической функцией плотности имеет кривую вращения, приближающуюся к наблюдаемой кривой вращения галактики Млечный Путь

3. Подбор функции плотности

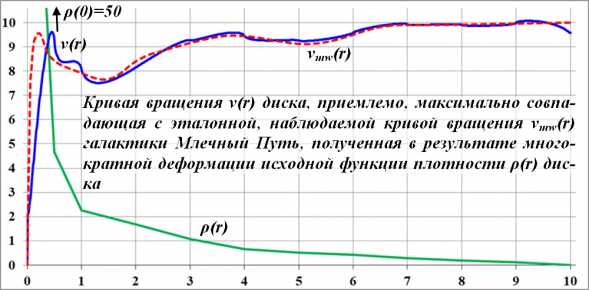
Рис.3.6. Подобранная функция плотности ρ(r) и соответствующая ей кривая вращения v(r) приемлемо, максимально совпадающая с эталонной, наблюдаемой кривой вращения vmw(r) галактики Млечный Путь

Результат, совпадение кривых вращения на рис.3.6 следует признать хорошим. Некоторые специфические отклонения в начале и конце кривых можно объяснить. На начальном этапе достичь хорошей точности не позволяет дискретность графика. Первые 10 точек выводятся с погрешностью от 10 до 200%. Например, различия между первым и вторым шагами двукратные. В конечной точке график кривой вращения диска связан со сложностью подбора функции плотности. Интервал слишком длинный для достаточно подробной детализации функции.

Вместе с тем следует учесть и ещё одно немаловажное обстоятельство: аппроксимируемая наблюдаемая кривая вращения галактики Млечный Путь сама построена с довольно большой погрешностью.

Из проведённых вычислений можно сделать вывод. Следует признать принципиальную возможность формирования такой функции плотности диска, изменения его радиальной плотности, которая позволяет получить любую заданную наперёд форму кривой вращения. В частности, сформированная выше вполне реальная функция плотности диска позволяет получить кривую вращения, предельно совпадающую с наблюдаемой кривой вращения галактики Млечный Путь. Следовательно, существуют такие же функции плотности диска, соответствующие кривым вращения других галактик.

Что непосредственно касается взятой за эталон галактики Млечный Путь, то построить для неё фактическую функцию плотности, видимо, технически возможно. Судя по всему, необходимые для вычислений основные параметры всех её составляющих известны: координаты звёзд и их массы. Вполне возможно построить график сил, действующих на некоторую звезду, параметры движения которой, предположительно, не соответствуют законам Кеплера. Понятно, что для этого потребуется произвести вычисления её силовых взаимодействий с несколькими миллиардами остальных звёзд галактики. Такие вычисления являются эквивалентом расчётов по плотности, причём в них усреднённая плотность представлена в точном дискретном виде, в виде пар звезда-звезда. Серьёзную трудность при таких расчётах составит, видимо, учёт масс газопылевых объектов. Вычисленная сила для проблемной звезды даст точное значение её фактической скорости, соответствует ли она её устойчивому орбитальному движению.

Выводы

В наших вычислениях мы не рассматривали диск как полный аналог какой-либо галактики. Тем не менее, то, что его кривую вращения удалось достаточно точно приблизить по форме к кривой вращения галактики Млечный Путь, свидетельствует о возможности формирования любой кривой вращения галактики, любой галактики исключительно за счёт специфического распределения её внутренней массы. То, что возможно для абстрактного, но физически возможного объекта, несомненно, должно быть возможно и для физического объекта реального.

Для достижения поставленной цели – формирования заданной формы кривой вращения – мы не использовали никаких внешних, скрытых сил или субстанций. Все без исключения "странности", возникшие в процессе вычислений, не являются противоречиями, все они нашли логическое объяснение.